Torsiestijfheid is een fundamentele technische parameter. Het is het vermogen van een constructiedeel om onder torsie weerstand te bieden tegen verdraaiing. Het is een cruciale, waardevolle eigenschap voor componenten die worden belast door torsiebelasting voor toepassingen zoals assen, balken en andere mechanische onderdelen die worden gebruikt in auto's, ruimtevaart, civiele bouw enz. Kennis van torsiestijfheid is cruciaal voor het bepalen van de sterkte en stabiliteit van deze onderdelen omdat het een directe invloed heeft op hun torsiesterkte en duurzaamheid.
Definitie en betekenis van torsiestijfheid in engineering
Torsiestijfheid wordt aangeduid met het symbool GJwaarbij G staat voor de afschuifmodulus van het materiaal, en J verwijst naar het polaire traagheidsmoment van de dwarsdoorsnede. Het vertegenwoordigt de hoeveelheid torsie die nodig is om een eenheidsverdraaiing per eenheidslengte van het constructiedeel te genereren.
De torsiestijfheid geeft de mate van verdraaiing van de structuur aan zonder schade. Torsiestijfheid is van vitaal belang voor engineering omdat het helpt bij het ontwikkelen van onderdelen die hun geometrie en prestaties moeten behouden onder omstandigheden van torsiebelasting.
Het is waardevol wanneer het wordt toegepast waar nauwkeurigheid en sterkte kritisch zijn, zoals lagers van mechanische constructies, propellers en dragende liggers.
Basisconcepten en fysische interpretatie
Om torsiestijfheid te begrijpen, moet je denken aan een cilindrische as onder torsie.
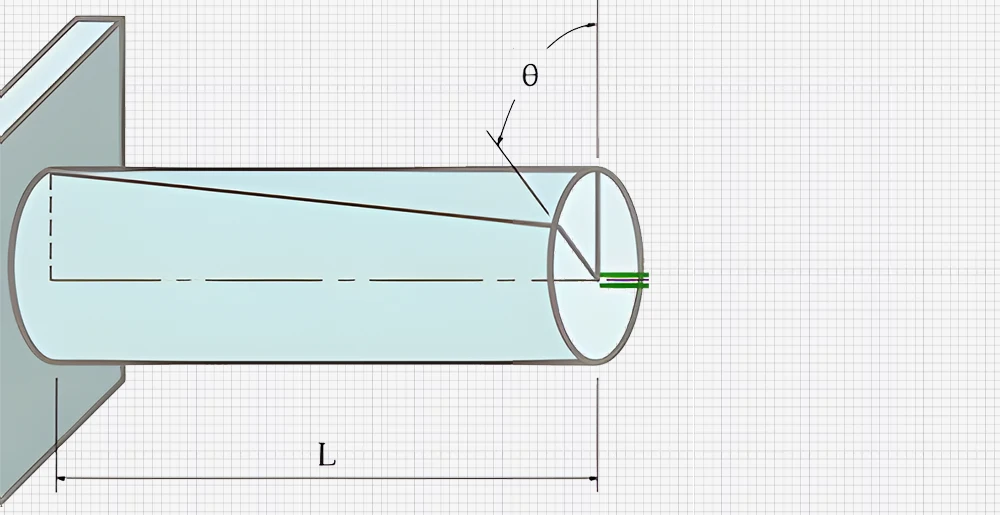
Het verband tussen het toegepaste koppel (T), de verdraaiingshoek (θ) en de aslengte (L) wordt als volgt uitgedrukt:
θ=TL/GJ
Uit deze vergelijking blijkt dat de verdraaiingshoek recht evenredig is met het koppel en de lengte van de as. Hij is omgekeerd evenredig met de torsiestijfheid GJ. De torsiestijfheid (GJ) is de weerstand van een as tegen verdraaiing onder een toegepast koppel. Hoe groter de torsiestijfheid, hoe kleiner de resulterende verdraaiingshoek bij een gegeven torsie. Hoe hoger de G- en J-waarden, hoe minder de as zal torderen.
Functioneel gezien gebruiken ingenieurs torsiestijfheid in hun toepassingen, waarbij ze inschatten hoe de component zal verdraaien onder een bepaalde belasting en bepalen of de verdraaiing voldoende is om een defect in de constructie te rechtvaardigen of de uitvoering van een specifieke functie te belemmeren.
Fundamentele principes van torsiestijfheid
Torsiestijfheid is fundamenteel bij het ontwerpen en analyseren van assen, tandwielen en constructies onder torsiebelasting. Het gaat hierbij om het vermogen van een materiaal en de constructie om weerstand te bieden aan de toegepaste torsie of torsiekracht en dit is afhankelijk van de eigenschappen van het materiaal en de dwarsdoorsnede van het onderdeel. Kennis van deze principes is cruciaal voor ingenieurs om componenten te ontwerpen die torsiebelastingen kunnen weerstaan zodat ze niet vervormen of bezwijken.
Materiaaleigenschappen die de torsiestijfheid beïnvloeden
De torsiestijfheid van een onderdeel hangt af van de afschuifmodulus G van het materiaal in kwestie. Dit is een maat voor de stijfheid van het materiaal bij afschuifspanning. De afschuifmodulus van verschillende materialen varieert evenredig. Staal heeft een hogere afschuifmodulus dan aluminium of polymeren, die flexibelere materiaalsoorten zijn. De afschuifmodulus is een van de materiaalconstanten. Deze hangt af van de soort atoombinding en het rooster van het materiaal.
| Vulstof Inhoud (wt%) | Matrixkristalliniteit (%) | G*(MPa) | σy(MPa) ±0,5 MPa | εr(%) ±(80%) | |
| PE | 0 | 52 | 2.8 | 16 | 1100 |
| PE-Calciet | 9.6 | 48 | 3.2 | 16 | 720 |
| PE-Calciet-SA | 7.7 | 48 | 3.1 | 15 | 720 |
| PE-Aragoniet | 10.3 | 51 | 3.45 | 15 | 910 |
| PE-Aragoniet-SA | 9.3 | 53 | 2.6 | 16 | 930 |
| PE-C.Fornicata | 8.6 | 49 | 2.8 | 16 | 670 |
| PE-C.Fornicata-SA | 9.5 | 49 | 3 | 15 | 740 |
| PE-C.Gigas | 6.5 | 52 | 2.8 | 16 | 730 |
| PE-C.Gigas-SA | 9.3 | 50 | 3.2 | 15 | 830 |
| PE-P.Maximus | 10.8 | 47 | 3 | 16 | 680 |
| PE-P.Maximus-SA | 9.7 | 50 | 3.2 | 16 | 760 |
Vergelijkingstabel van de vloeigrens, treksterkte (UTS) en elasticiteitsmodulus voor verschillende materialen
| Materiaal | Opbrengststerkte (MPa) | UTS (MPa) | Young's Modulus (GPa) |
| Aluminium | 35 | 90 | 69 |
| Koper | 69 | 200 | 117 |
| Messing | 75 | 300 | 120 |
| IJzer | 130 | 262 | 170 |
| Nikkel | 138 | 480 | 210 |
| Staal | 180 | 380 | 200 |
| Titanium | 450 | 520 | 110 |
| Molybdeen | 565 | 655 | 330 |
| Zirkoniumlegering (typische bekleding) | 380 | 510 | 99 |
| 08Kh18N10T roestvrij staal | 216 | 530 | 196 |
| Gelegeerd 304L roestvrij staal | 241 | 586 | 193 |
| SA-508 Gr.3 Cl.2 (laag gelegeerd ferritisch staal) | 500 | 700 | 210 |
| 15Kh2NMFA (laag gelegeerd ferritisch staal) | 490 | 610 | 220 |
Een andere materiaaleigenschap die van invloed is op de torsiestijfheid is de uniformiteit of homogeniteit van het materiaal en de mate waarin het materiaal anisotroop of isotroop is. De isotrope eigenschap zorgt ervoor dat de torsiestijfheid constant is in alle richtingen in isotroop materiaal.
In anisotrope materialen, bijvoorbeeld composieten, kan de torsiestijfheid verschillen op basis van de positie van de torsietoepassing ten opzichte van de materiaalafzetting.
Een andere kritieke factor die de torsiestijfheid beïnvloedt, is de materiaalkeuze voor de toepassing. Ingenieurs kunnen bijvoorbeeld kiezen voor composietmaterialen met een hoge stijfheid-gewichtsverhouding in ontwerpgebieden waar torsiestijfheid en een laag gewicht van cruciaal belang zijn.
Torsiestijfheid in verschillende geometrische vormen
Torsiestijfheid, gekarakteriseerd door het polaire traagheidsmoment, houdt in redelijke mate rekening met de geometrie van de dwarsdoorsnede van een component. Het polaire traagheidsmoment is een geometrisch concept dat verwijst naar de oppervlakteverdeling van de dwarsdoorsnede ten opzichte van de rotatieas. Verschillende materialen hebben verschillende waarden van J, vandaar verschillende torsiestijfheden van de dwarsdoorsnedevormen.
Cirkelvormige doorsneden:
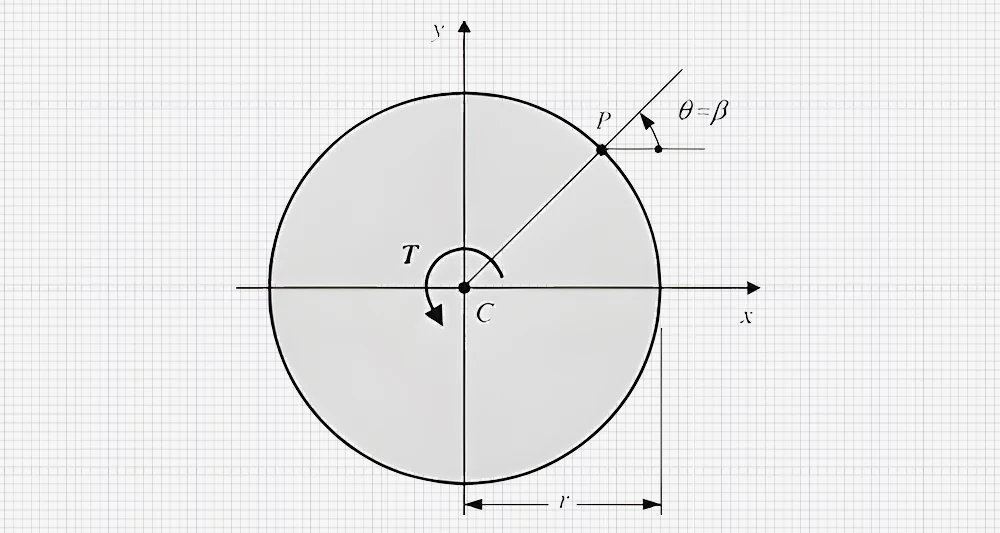
Cirkelvormige assen komen vaak voor in de machinebouw. Ze hebben een symmetrische verdeling van materiaal in het dwarsdoorsnedevlak rond de draaias. Het polaire traagheidsmoment voor een massieve cirkelvormige as wordt bepaald door de formule:
J = (πr⁴)/2
waarbij 'r' de straal van de as voorstelt. Cirkelvormige doorsneden hebben een relatief klein tweede oppervlaktemoment, wat hun torsiestijfheid vergroot. Daarom worden ze gebruikt in assen en draaiende onderdelen van machines.
Voorbeeld 1
Voorbeeld 1
Stel dat een as een massieve as is met straal r = 5 cm en lengte L = 1 m voor de gegeven waarde afschuifmodulus G = 80 GPa.
- Bereken het polaire traagheidsmoment
- Bepaal de torsiestijfheid
- Als een koppel T=50 Nm wordt toegepast, bereken dan de draaihoek θ
Oplossing
J=(πr4)/2=π(0,05)4)/2=3,07×10-6m4GJ=80×109×3,07×10-6=245,6Nm2θ=TL/GJ=(50×1)/245.6=0.204 radians
Rechthoekige doorsneden:
De andere geometrische vorm van metalen staven is rechthoekig, wat van toepassing is in de techniek, met name constructies. Bij een rechthoekige staaf is de torsiestijfheid veel gecompliceerder en afhankelijk van de hoogte-breedteverhouding van de zijden van de doorsnede. Voor dunne rechthoekige doorsneden, waarbij de ene dimensie veel kleiner is dan de andere, kan het polaire traagheidsmoment benaderd worden door:
J = (ab³)/3
waarbij deze formule alleen geldig is als de dikte aanzienlijk kleiner is dan de breedte.
Hier, a en b zijn de afmetingen van de rechthoek die respectievelijk de lengte en de breedte meten. Bij gebruik als staal voor gebouwen en constructies zijn rechthoekige secties meestal minder torsiestijf dan cirkelvormige secties, vooral wanneer hun hoogte-breedteverhouding hoog is, wat aangeeft dat de ene zijde van de rechthoek langer is dan de andere.
Voorbeeld 2
Beschouw een rechthoekige, dunwandige stalen balk met afmetingen 20 cm bij 10 cm, een lengte van 3 meter en met afschuivingsmodulus G = 75 x 109 GPa. Bepaal de torsiestijfheid GJ en de draaihoek θ wanneer een torsie van T=2000Nm wordt toegepast.
Oplossing
Het polaire traagheidsmoment J voor een rechthoekige doorsnede wordt gegeven door:
J=(ab3)/3=(0.1×0.23)/3=2.67×10-4
Torsiestijfheid GJ=75×109×2.67×10-4=2×107Nm2
De draaihoek wordt gegeven door:
θ=(2000×3)/(2×107 =1.5×10-4 radialen
Holle en complexe doorsneden:
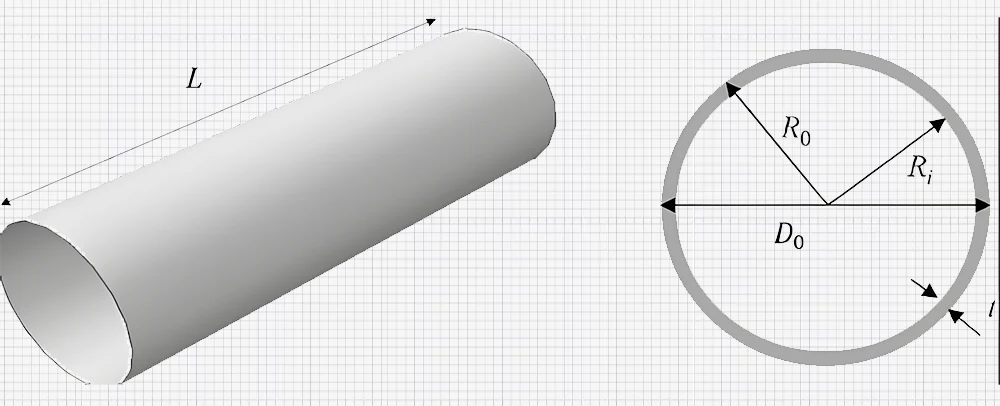
Holle cirkelvormige profielen zoals buizen zijn ook nuttig in de machinebouw, evenals niet-cirkelvormige profielen zoals I-profielen en T-profielen. Cilindrische schalen bieden een goede weerstand tegen torsiekrachten en zijn relatief licht - ze kunnen worden gebruikt in auto's als aandrijfassen of in gebouwen als balken. Het polaire traagheidsmoment voor een holle cirkelvormige doorsnede wordt gegeven door:
J=π(ro4-ri4)/2
Waar ro de buitenstraal is, en ri is de binnenstraal.
Voorbeeld 3
Veronderstel een lichte, dunwandige holle cirkelvormige schacht met buitenstraal 'r' = 5 cm, binnenstraal 'b' = 3 cm, lengte 'L' = 2 m en het materiaal met afschuifmodulus G = 70 G GPa.
- Bereken het polaire traagheidsmoment J
- Bepaal de torsiestijfheid van GJ
- Als een koppel T=30 Nm wordt toegepast, bereken dan de draaihoek θ
Oplossing
J=π(ro4-ri4)/2=π(0,054-0,034)/2=2,18×10-6m4GJ=70×109×2,18×10-6=152,6Nm2θ=TL/GJ=(30×2)/152,6
Torsiestijfheid in verschillende materialen
De torsiestijfheid hangt af van de materialen. Metalen met een hoge afschuifmodulus hebben inherent een hoge torsiestijfheid. Staal heeft bijvoorbeeld een afschuifmodulus van 80 GPa en is nuttig op plaatsen met aanzienlijke torsiemomenten, zoals aandrijfassen en machines. De uniformiteit van metalen voorkomt variaties in de torsiestijfheid van het materiaal, waardoor het voorspelbare prestaties kan leveren in situaties die een hoge nauwkeurigheid en belastbaarheid vereisen.
Polymeren hebben echter een relatief lage afschuifmodulus, variërend van 0,5 tot 3 GPa, wat leidt tot een lage torsiestijfheid. Deze eigenschap maakt polymeren kwetsbaarder voor verdraaiing onder belasting.
Toch kunnen hun flexibiliteit en elasticiteit hen ten goede komen wanneer een bepaalde mate van vervorming toelaatbaar is. Ze zijn bijvoorbeeld nuttig bij flexibele koppelingen. Als we de torsiestijfheid van een metalen staaf en een polymeerstaaf vergelijken door hetzelfde koppel toe te passen, dan is de hoek bij de laatste relatief groter. Dit bewijst het verschil in torsiestijfheid van twee van dergelijke materialen.
Composieten bieden daarentegen het voordeel van afstembare eigenschappen, waarbij de torsiestijfheid afhankelijk is van de vezel- en matrixmaterialen. Hoewel composieten een hoog stijfheidspotentieel hebben, is bekend dat deze structuren anisotroop gedrag vertonen. Dit betekent dat de stijfheid afhankelijk is van de richting van de belasting. De uitlijning van de vezelversterking is van vitaal belang en vereist een nauwkeurige oriëntatie voor optimale prestaties. Bovendien kunnen de torsiestijfheidseigenschappen ook variëren in heterogene materialen zoals composieten en zijn ze mogelijk niet consistent in alle delen van de doorsnede.
Tabel 1: Vergelijking van torsiestijfheid in metalen, polymeren en composieten
| Type materiaal | Voorbeeld Materiaal | Afschuifmodulus (G) in GPa | Polair traagheidsmoment (J)( ×10-6m4 | Torsiestijfheid (GJ) In Nm2 | Relatieve dichtheid (kg/m³) | Algemene toepassingen |
| Metaal | Staal (AISI 1045) | 80 | 5 | 400 | 7050 | Aandrijfassen, tandwielen, machineonderdelen |
| Metaal | Aluminium (6061-T6) | 26 | 4 | 104 | 2700 | Vliegtuigonderdelen, auto-onderdelen |
| Polymeer | Polyethyleen (HDPE) | 0.8 | 3 | 2.4 | 950 | Buizen, flexibele koppelingen |
| Polymeer | Polycarbonaat (PC) | 2.3 | 3.5 | 8.05 | 1200 | Veiligheidshelmen, autoruiten |
| Samengesteld | CFRP | 100 | 6 | 600 | 1600 | Ruimtevaartonderdelen, hoogwaardige sportuitrusting |
| Samengesteld | CFRP | 25 | 4.5 | 112.5 | 1850 | Marine-onderdelen, autopanelen |
Torsiestijfheid in bouwkunde
Torsiestijfheid in wolkenkrabbers en bruggen
Rotatiestijfheid is een cruciaal element in technische constructies, vooral bij de bouw van wolkenkrabbers en bruggen. Een factor in engineering is dat de constructie in staat moet zijn om belastingen te verwerken zonder te verdraaien.
Voor de bouw van gebouwen of bruggen is het wenselijk om een torsiestijfheidswaarde te hebben die kan helpen om krachten in een lateraal vlak te weerstaan, zoals wind- of aardbevingskrachten.
Hoge gebouwen en uitkragende bruggen moeten bijvoorbeeld voldoende torsiestijfheid bezitten om verdraaiing tegen te gaan, wat kan leiden tot verschijnselen zoals instorting. De manier waarop de vorm van het gebouw of de brug wordt geformuleerd en het patroon van massa en stijfheid zijn gebruikelijk om het torsie-effect te minimaliseren.


Het belang van torsiestijfheid in balken en kolommen
Torsiestijfheid is ook essentieel in balken en kolommen. Deze constructiedelen moeten bestand zijn tegen torsiemomenten en de belastingen kunnen dragen. Elk lid dat onderhevig is aan torsiespanning, zoals uitkragende liggers of asymmetrisch belaste liggers, mag in geen geval te veel torderen.
Op dezelfde manier moeten de kolommen ook ontworpen worden om eventuele torsiemomenten op te nemen die kunnen ontstaan door excentriciteit in de belasting of laterale krachten. De torsiestijfheid van deze elementen kan afhangen van de vorm van de dwarsdoorsnede van deze elementen, de gebruikte materialen en de ondersteuningsomstandigheden.
Vergelijk bijvoorbeeld twee staven met dezelfde dwarsdoorsnede. Staven met een cirkelvormige dwarsdoorsnede zijn in de regel beter bestand tegen verdraaiing dan rechthoekige staven.
Voorbeelden uit de praktijk en ontwerpstrategieën
Waarnemingen van echte scenario's van torsiefouten bewijzen dat torsiestijfheid een kritische overweging vereist in engineering. Zo stortte de Tacoma Narrows Bridge, in de volksmond bekend als 'Galloping Gertie', in 1940 in, voornamelijk als gevolg van aerodynamische flutter. Ontoereikende torsiestijfheid droeg echter indirect bij aan het falen onder specifieke windomstandigheden.

Ontwerpers kunnen verschillende strategieën toepassen om torsiekwesties te verminderen tijdens het ontwerpen van constructies. Ze kunnen bijvoorbeeld doorsneden stijver maken. Het uitbreiden van verstevigingssystemen die van dienst kunnen zijn in de strijd tegen torsie, evenals het inzetten van superieure composietmaterialen en -technologie in de constructietechniek om torsieprestaties te verbeteren, is van cruciaal belang. Engineeringpraktijken omvatten tegenwoordig ook computationele technieken bij het analyseren van torsiebelastingen en het ontwikkelen van constructies die torsiebelastingen kunnen dragen zonder de structurele integriteit en functionaliteit aan te tasten.
De rol van torsiestijfheid in werktuigbouwkunde
Torsiestijfheid is nuttig in de machinebouw voor verschillende onderdelen van machines, zoals assen, tandwielen en koppelingen. Het zorgt ervoor dat assen slechts een klein beetje buigen onder het torsiemoment, zodat de apparatuur correct kan functioneren. Daarom is torsiestijfheid in assen cruciaal om torsie te voorkomen die de mechanische prestaties of de krachtoverbrenging negatief zou kunnen beïnvloeden.
Op dezelfde manier is de werking van tandwielen afhankelijk van torsiestijfheid om te zorgen dat ze goed in elkaar grijpen en de belasting goed verdelen tijdens de werking. Voldoende torsiestijfheid in tandwielen voorkomt ook slip en zorgt voor een goede krachtoverbrenging tussen de tandwielen. In auto's en vliegtuigen verhoogt torsiestijfheid de efficiëntie, prestaties en veiligheid van het voertuig.
In de autotechniek bijvoorbeeld zijn de stationaire onderdelen van de aandrijflijn en de motor ontworpen om hoge torsiebelastingen te dragen tijdens het gebruik.
Conclusie
Torsiestijfheid is een essentiële factor bij het ontwerpen en fabriceren van onderdelen in de bouwkunde, werktuigbouwkunde, civiele techniek en nog veel meer. Het beschrijft het vermogen van een materiaal of constructie om torsiekracht onder torsie te verdragen. Het specificeert de stabiliteit van onderdelen voor roterende spanningen. Torsiestijfheid betekent de stijfheid in termen van weerstand tegen verdraaiing in een gekozen vlak.
De materiaaleigenschappen, de geometrie van de constructiedelen en de specifieke gebruiksomstandigheden helpen ingenieurs om een optimale oplossing te vinden voor ontwerpproblemen. Torsiestijfheid is gunstig op structureel en mechanisch gebied om laterale krachten tegen te gaan voor structurele stabiliteit of het functioneren van mechanische apparatuur.
Zo kunnen ingenieurs systemen ontwerpen die meeveranderen met de bediening en de algemene functionaliteit verbeteren door problemen met materialen en geometrische vormen te identificeren. In de toekomst, naarmate er meer engineeringtechnologieën komen, zal de verdere optimalisatie en integratie van torsiestijfheidsprincipes de veiligheid en prestaties van technische systemen verbeteren.