La rigidità torsionale è un parametro ingegneristico fondamentale. È la capacità di un elemento strutturale, sottoposto a coppia, di resistere alla torsione. È una caratteristica cruciale e preziosa per i componenti sottoposti a carichi torsionali per applicazioni come alberi, travi e altre parti meccaniche utilizzate nel settore automobilistico, aerospaziale, delle costruzioni civili, ecc. La conoscenza della rigidità torsionale è fondamentale per determinare la resistenza e la stabilità di questi componenti, poiché influisce direttamente sulla loro resistenza torsionale e sulla loro durata.
Definizione e significato della rigidità torsionale in ingegneria
La rigidità torsionale è indicata con il simbolo GJ, dove G indica il modulo di taglio del materiale, e J si riferisce al momento d'inerzia polare della sezione trasversale. Rappresenta la quantità di coppia necessaria per generare una torsione unitaria per unità di lunghezza dell'elemento strutturale.
La rigidità torsionale indica il grado di torsione della struttura senza subire danni. La rigidità torsionale è fondamentale in ingegneria, in quanto aiuta a sviluppare componenti che devono mantenere la loro geometria e le loro prestazioni in condizioni di carico torsionale.
È preziosa quando si applica in situazioni in cui la precisione e la resistenza sono fondamentali, come i cuscinetti delle strutture meccaniche, le eliche e le travi portanti.
Concetti di base e interpretazione fisica
Per comprendere la rigidità torsionale, occorre pensare a un albero cilindrico sottoposto a coppia.
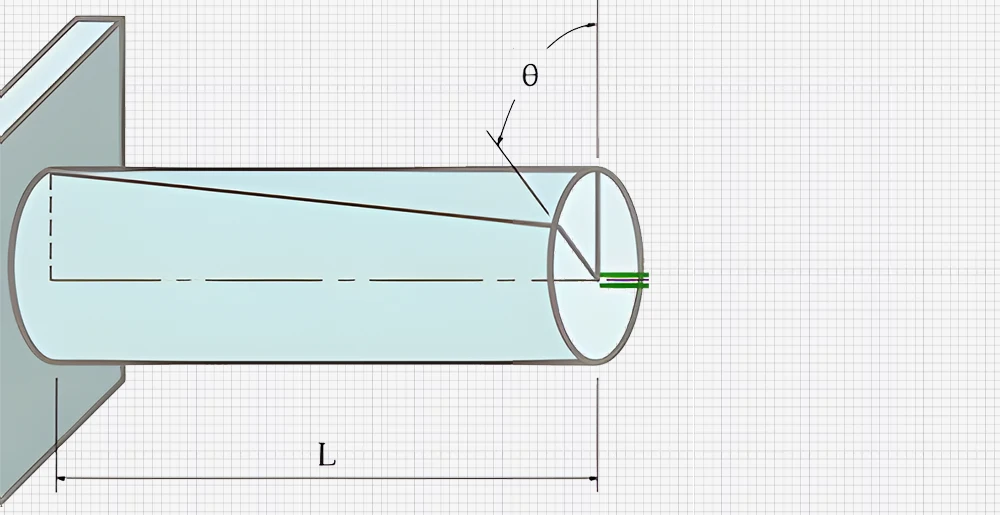
Il legame tra la coppia applicata (T), l'angolo di torsione (θ) e la lunghezza dell'albero (L) è espresso come segue:
θ=TL/GJ
Da questa equazione si evince che l'angolo di torsione è direttamente proporzionale alla coppia e alla lunghezza dell'albero. È inversamente proporzionale alla rigidità torsionale GJ. La rigidità torsionale (GJ) rappresenta la resistenza di un albero alla torsione in presenza di una coppia applicata. Maggiore è la rigidità torsionale, minore è l'angolo di torsione risultante per una data coppia. Più alti sono i valori di G e J, meno l'albero si torcerà.
Dal punto di vista funzionale, gli ingegneri utilizzano la rigidità torsionale nelle loro applicazioni, stimando la torsione del componente sotto un particolare carico e determinando se la torsione è sufficiente a giustificare un cedimento della struttura o a ostacolare lo svolgimento di una funzione specifica.
Principi fondamentali della rigidità torsionale
La rigidità torsionale è fondamentale nella progettazione e nell'analisi di alberi, ingranaggi e strutture sottoposti a carichi torsionali. Si tratta della capacità di un materiale e della sua struttura di resistere all'applicazione di una coppia o di una forza di torsione e dipende dalle caratteristiche del materiale e dall'area della sezione trasversale dell'elemento. La conoscenza di questi principi è fondamentale per gli ingegneri che devono progettare componenti in grado di resistere ai carichi torsionali in modo che non si deformino o si guastino.
Proprietà del materiale che influenzano la rigidità torsionale
La rigidità torsionale di un componente dipende dal modulo di taglio G del materiale in esame. Si tratta di una misura della rigidità del materiale in presenza di sollecitazioni di taglio. Il modulo di taglio dei diversi materiali è altrettanto variabile. L'acciaio possiede un modulo di taglio più elevato rispetto all'alluminio o ai polimeri, che sono tipi di materiali più flessibili. Il modulo di taglio è una delle costanti del materiale. Dipende dal tipo di legame atomico e dal reticolo del materiale.
| Contenuto di riempimento (wt%) | Cristallinità della matrice (%) | G*(MPa) | σy(MPa) ±0,5 MPa | εr(%) ±(80%) | |
| PE | 0 | 52 | 2.8 | 16 | 1100 |
| PE-Calcite | 9.6 | 48 | 3.2 | 16 | 720 |
| PE-Calcite-SA | 7.7 | 48 | 3.1 | 15 | 720 |
| PE-Aragonite | 10.3 | 51 | 3.45 | 15 | 910 |
| PE-Aragonite-SA | 9.3 | 53 | 2.6 | 16 | 930 |
| PE-C.Fornicata | 8.6 | 49 | 2.8 | 16 | 670 |
| PE-C.Fornicata-SA | 9.5 | 49 | 3 | 15 | 740 |
| PE-C.Gigas | 6.5 | 52 | 2.8 | 16 | 730 |
| PE-C.Gigas-SA | 9.3 | 50 | 3.2 | 15 | 830 |
| PE-P.Maximus | 10.8 | 47 | 3 | 16 | 680 |
| PE-P.Maximus-SA | 9.7 | 50 | 3.2 | 16 | 760 |
Tabella di confronto tra carico di snervamento, carico di rottura (UTS) e modulo di Young per i diversi materiali
| Materiale | Resistenza allo snervamento (MPa) | UTS (MPa) | Modulo di Young (GPa) |
| Alluminio | 35 | 90 | 69 |
| Rame | 69 | 200 | 117 |
| Ottone | 75 | 300 | 120 |
| Ferro | 130 | 262 | 170 |
| Nichel | 138 | 480 | 210 |
| Acciaio | 180 | 380 | 200 |
| Titanio | 450 | 520 | 110 |
| Molibdeno | 565 | 655 | 330 |
| Lega di zirconio (rivestimento tipico) | 380 | 510 | 99 |
| 08Kh18N10T acciaio inox | 216 | 530 | 196 |
| Acciaio inossidabile in lega 304L | 241 | 586 | 193 |
| SA-508 Gr.3 Cl.2 (acciaio ferritico a bassa lega) | 500 | 700 | 210 |
| 15Kh2NMFA (acciaio ferritico a bassa lega) | 490 | 610 | 220 |
Un'altra proprietà del materiale che influenza la rigidità torsionale è l'uniformità o l'omogeneità del materiale e la misura in cui il materiale è anisotropo o isotropo. La proprietà dell'isotropia consente alla rigidità torsionale di essere costante in tutte le direzioni in un materiale isotropo.
Nei materiali anisotropi, ad esempio i compositi, la rigidità torsionale può variare in base alla posizione dell'applicazione della coppia rispetto al deposito del materiale.
Un altro fattore critico che influisce sulla rigidità torsionale è la scelta del materiale per l'applicazione. Ad esempio, gli ingegneri possono optare per materiali compositi ad alto rapporto rigidità/peso in aree di progettazione in cui la rigidità torsionale e il peso ridotto sono fondamentali.
Rigidità torsionale in diverse forme geometriche
La rigidità torsionale, caratterizzata dal momento d'inerzia polare, considera in misura ragionevole la geometria della sezione trasversale di un componente. Il momento d'inerzia polare è un concetto geometrico che si riferisce alla distribuzione dell'area della sezione trasversale rispetto all'asse di rotazione. Materiali diversi hanno valori diversi di J, quindi diverse rigidità torsionali delle forme trasversali.
Sezioni trasversali circolari:
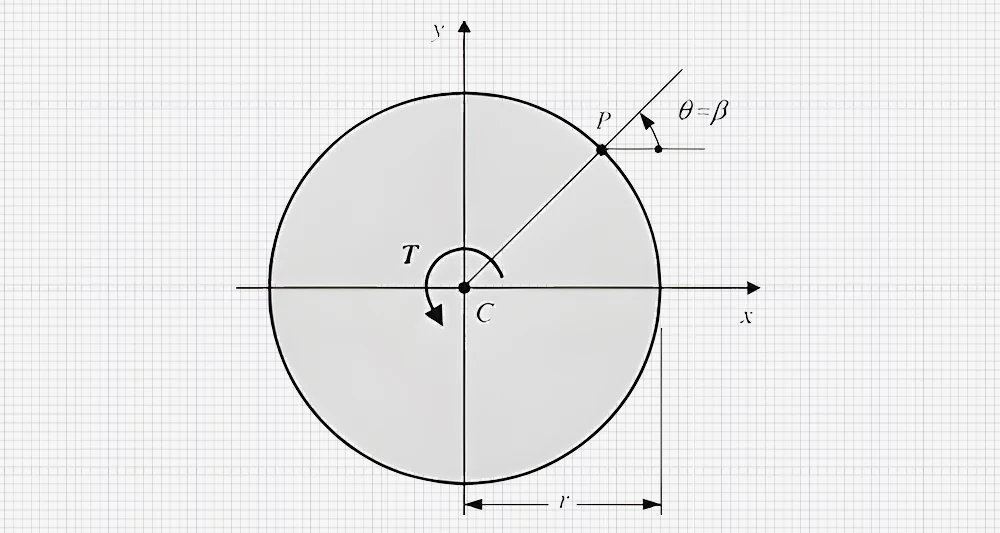
Gli alberi circolari sono comuni nel campo dell'ingegneria. Hanno una distribuzione simmetrica del materiale nel piano della sezione trasversale attorno all'asse di rotazione. Il momento d'inerzia polare di un albero circolare solido è determinato dalla formula:
J = (πr⁴)/2
dove "r" rappresenta il raggio dell'albero. Le sezioni trasversali circolari hanno un secondo momento d'area relativamente piccolo, che ne aumenta la rigidità torsionale. Per questo motivo, sono utilizzate negli alberi e nelle parti rotanti delle macchine.
Esempio 1
Esempio 1
Supponiamo che un albero sia un albero solido con raggio r = 5 cm e lunghezza L = 1 m per il valore dato del modulo di taglio G = 80 GPa.
- Calcolare il momento d'inerzia polare
- Determinare la rigidità torsionale
- Se viene applicata una coppia T=50 Nm, calcolare l'angolo di torsione θ
Soluzione
J=(πr4)/2=π(0,05)4)/2=3,07×10-6m4GJ=80×109×3,07×10-6=245,6Nm2θ=TL/GJ=(50×1)/245.6=0.204 radians
Sezioni trasversali rettangolari:
L'altra forma geometrica delle barre metalliche è quella rettangolare, applicabile in ingegneria, in particolare nelle strutture. Con una barra rettangolare, la rigidità torsionale è molto più complicata e dipende dal rapporto di aspetto dei lati della sezione trasversale. Per le sezioni rettangolari sottili, dove una dimensione è molto più piccola dell'altra, il momento d'inerzia polare può essere approssimato da:
J = (ab³)/3
dove questa formula è valida solo quando lo spessore è significativamente più piccolo della larghezza.
Qui, a e b sono le dimensioni del rettangolo che misurano rispettivamente la lunghezza e la larghezza. Quando vengono utilizzati come elementi in acciaio per edifici e strutture, i profilati rettangolari sono solitamente meno rigidi alla torsione rispetto ai profilati circolari, soprattutto quando il loro rapporto d'aspetto è elevato, il che significa che un lato del rettangolo è più allungato dell'altro.
Esempio 2
Si consideri una trave rettangolare in acciaio a pareti sottili di dimensioni 20 cm per 10 cm, lunga 3 metri e con modulo di taglio G = 75 x 109 GPa. Determinare la rigidità torsionale GJ e l'angolo di torsione θ quando viene applicata una coppia T=2000Nm.
Soluzione
Il Momento d'inerzia polare J per una sezione rettangolare è dato da:
J=(ab3)/3=(0.1×0.23)/3=2.67×10-4
Rigidità torsionale GJ=75×109×2.67×10-4=2×107Nm2
L'angolo di torsione è dato da:
θ=(2000×3)/(2×107 =1.5×10-4 radianti
Sezioni trasversali cave e complesse:
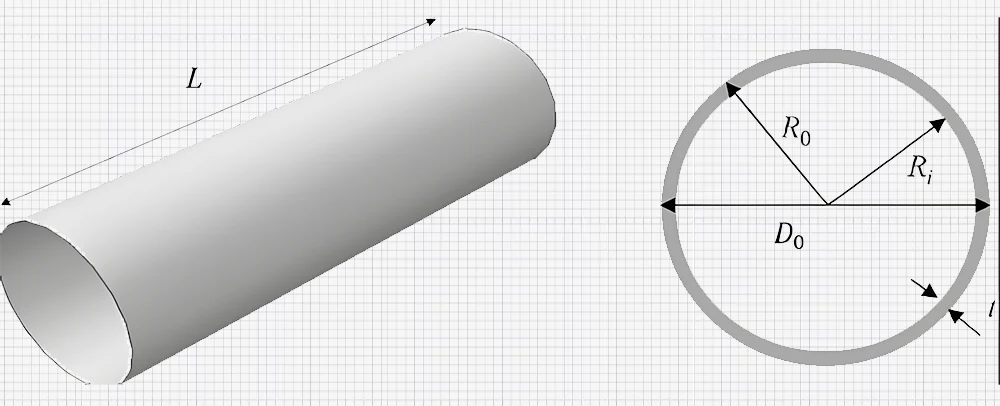
Anche le sezioni circolari cave, come i tubi, sono utili in ingegneria, così come le sezioni non circolari, come le travi a I e a T. I gusci cilindrici offrono una buona resistenza alle forze di torsione e sono relativamente leggeri: possono essere utilizzati nelle automobili come alberi di trasmissione o negli edifici come travi. Il momento d'inerzia polare di una sezione circolare cava è dato da:
J=π(ro4-ri4)/2
Dove ro è il raggio esterno e ri è il raggio interno.
Esempio 3
Si supponga un albero circolare cavo leggero e a parete sottile con raggio esterno "r" = 5 cm, raggio interno "b" = 3 cm, lunghezza "L" = 2 m e materiale con modulo di taglio G = 70 G GPa.
- Calcolare il momento d'inerzia polare J
- Determinare la rigidità torsionale di GJ
- Se viene applicata una coppia T=30 Nm, calcolare l'angolo di torsione θ
Soluzione
J=π(ro4-ri4)/2=π(0,054-0,034)/2=2,18×10-6m4GJ=70×109×2,18×10-6=152,6Nm2θ=TL/GJ=(30×2)/152,6
Rigidità torsionale in diversi materiali
La rigidità torsionale dipende dai materiali. I metalli, avendo un elevato modulo di taglio, hanno intrinsecamente un'elevata rigidità torsionale. Ad esempio, l'acciaio ha un modulo di taglio di 80 GPa ed è utile in luoghi con momenti di torsione significativi, come gli alberi di trasmissione e le macchine. L'uniformità dei metalli impedisce variazioni nella rigidità torsionale del materiale, consentendo di fornire prestazioni prevedibili in situazioni che richiedono un'elevata precisione e capacità di carico.
Tuttavia, i polimeri hanno un modulo di taglio relativamente basso, compreso tra 0,5 e 3 GPa, che comporta una bassa rigidità torsionale. Questa caratteristica rende i polimeri più vulnerabili alla torsione sotto carico.
Tuttavia, la loro flessibilità ed elasticità può essere utile quando è consentito un certo grado di deformazione. Ad esempio, sono utili nell'accoppiamento flessibile. Confrontando lo stato di torsione di un'asta metallica e di un'asta polimerica con l'applicazione della stessa coppia, l'angolo è relativamente più significativo in quest'ultima. Ciò dimostra la differenza di rigidità torsionale di questi due materiali.
Al contrario, i compositi offrono il vantaggio di caratteristiche regolabili, con una rigidità torsionale che dipende dai materiali delle fibre e della matrice. Sebbene i compositi possano avere un elevato potenziale di rigidità, è noto che queste strutture hanno un comportamento anisotropo. Ciò implica che la rigidità dipende dalla direzione del carico. L'allineamento delle fibre di rinforzo è fondamentale e richiede un orientamento preciso per ottenere prestazioni ottimali. Inoltre, le caratteristiche di rigidità torsionale possono variare anche in materiali eterogenei come i compositi e possono non essere coerenti in tutte le parti della sezione trasversale.
Tabella 1: confronto tra la rigidità torsionale di metalli, polimeri e compositi
| Tipo di materiale | Esempio di materiale | Modulo di taglio (G) in GPa | Momento d'inerzia polare (J)( ×10-6m4 | Rigidità torsionale (GJ) In Nm2 | Densità relativa (kg/m³) | Applicazioni comuni |
| Metallo | Acciaio (AISI 1045) | 80 | 5 | 400 | 7050 | Alberi di trasmissione, ingranaggi, parti di macchine |
| Metallo | Alluminio (6061-T6) | 26 | 4 | 104 | 2700 | Componenti per aerei, parti di automobili |
| Polimero | Polietilene (HDPE) | 0.8 | 3 | 2.4 | 950 | Tubi, giunti flessibili |
| Polimero | Policarbonato (PC) | 2.3 | 3.5 | 8.05 | 1200 | Caschi di sicurezza, vetri per autoveicoli |
| Composito | CFRP | 100 | 6 | 600 | 1600 | Componenti aerospaziali, attrezzature sportive ad alte prestazioni |
| Composito | CFRP | 25 | 4.5 | 112.5 | 1850 | Componenti marini, pannelli automobilistici |
Rigidità torsionale nell'ingegneria strutturale
Rigidità torsionale di grattacieli e ponti
La rigidità rotazionale è un elemento cruciale nelle strutture ingegneristiche, in particolare nella costruzione di grattacieli e ponti. Un fattore di ingegneria è che la struttura deve essere in grado di gestire i carichi senza subire torsioni.
Per la costruzione di edifici o ponti, è auspicabile avere un valore di rigidità torsionale che possa aiutare a resistere a forze che si trovano su un piano laterale, come quelle del vento o del terremoto.
Ad esempio, gli edifici alti e i ponti a sbalzo devono possedere un'adeguata rigidità torsionale per resistere alla torsione, che può provocare fenomeni come il crollo. Il modo di formulare la forma dell'edificio o del ponte e lo schema di massa e rigidezza sono abituali per minimizzare l'effetto torsionale.


Importanza della rigidità torsionale di travi e colonne
La rigidità torsionale è essenziale anche per le travi e le colonne. Questi elementi strutturali devono avere la capacità di resistere ai momenti torcenti e di sostenere i carichi. Qualsiasi elemento soggetto a sollecitazioni torsionali, come gli sbalzi o le travi caricate asimmetricamente, non può in alcun modo subire torsioni eccessive.
Allo stesso modo, anche le colonne devono essere progettate per supportare eventuali momenti torsionali che potrebbero verificarsi a causa dell'eccentricità del carico o delle forze laterali. La rigidità torsionale di questi elementi può dipendere dalla forma della sezione trasversale di questi elementi, dai materiali utilizzati e dalle condizioni di supporto.
Ad esempio, confrontate due barre con la stessa sezione trasversale. Le barre a sezione circolare sono, di norma, più resistenti alla torsione rispetto a quelle rettangolari.
Esempi di vita reale e strategie di progettazione
L'osservazione di scenari reali di cedimento per torsione dimostra che la rigidità torsionale richiede una considerazione critica in ingegneria. Ad esempio, il Tacoma Narrows Bridge, noto come "Galloping Gertie", è crollato nel 1940 principalmente a causa del flutter aerodinamico. Tuttavia, una rigidità torsionale inadeguata ha contribuito indirettamente al cedimento in determinate condizioni di vento.

I progettisti possono applicare diverse strategie per ridurre i problemi torsionali durante la progettazione delle strutture. Ad esempio, possono rendere più rigide le sezioni trasversali. È fondamentale estendere i sistemi di controventatura che possono essere utili nella lotta contro la torsione, nonché impiegare materiali compositi e tecnologie superiori nell'ingegneria delle strutture per migliorare le prestazioni torsionali. Le pratiche ingegneristiche oggi coinvolgono anche le tecniche computazionali nell'analisi dei carichi torsionali e nello sviluppo di strutture in grado di sostenere i carichi torsionali senza compromettere l'integrità strutturale e la funzionalità.
Ruolo della rigidità torsionale nell'ingegneria meccanica
La rigidità torsionale è utile in ingegneria meccanica per diverse aree delle macchine, come alberi, ingranaggi e giunti. Garantisce che gli alberi si pieghino solo leggermente sotto il momento torcente per consentire il corretto funzionamento dell'apparecchiatura. Pertanto, la rigidità torsionale degli alberi è fondamentale per evitare torsioni che potrebbero avere un impatto negativo sulle prestazioni meccaniche o sulla trasmissione di potenza.
Allo stesso modo, il funzionamento degli ingranaggi si basa sulla rigidità torsionale per garantire il corretto ingranamento e la distribuzione del carico durante il funzionamento. Livelli adeguati di rigidità torsionale negli ingranaggi eliminano anche gli slittamenti, garantendo una corretta trasmissione di potenza tra gli ingranaggi. Nelle automobili e negli aerei, la rigidità torsionale aumenta l'efficienza, le prestazioni e la sicurezza del veicolo.
Ad esempio, nell'ingegneria automobilistica, i componenti fissi della trasmissione e del motore sono progettati per sostenere elevati carichi torsionali durante il funzionamento.
Conclusione
La rigidità torsionale è un fattore essenziale per la progettazione e la fabbricazione di componenti nell'ingegneria strutturale e meccanica, nell'ingegneria civile e molto altro. Descrive la capacità di un materiale o di una struttura di sopportare la forza di torsione in presenza di una coppia. Specifica la stabilità dei componenti alle sollecitazioni rotazionali. Per rigidità torsionale si intende la rigidità in termini di resistenza alla torsione in un piano prescelto.
Pertanto, le proprietà dei materiali, la geometria dei componenti strutturali e le condizioni specifiche di utilizzo aiutano gli ingegneri a trovare una soluzione ottimale per i problemi di progettazione. La rigidità torsionale è utile in campo strutturale e meccanico per contrastare le forze laterali per la stabilità della struttura o il funzionamento delle apparecchiature meccaniche.
In questo modo, gli ingegneri possono progettare sistemi che cambiano con l'intento di operare e migliorare la funzionalità generale identificando i problemi dei materiali e della forma geometrica. In futuro, con l'aumento delle tecnologie ingegneristiche, l'ulteriore ottimizzazione e incorporazione dei principi di rigidità torsionale aumenterà la sicurezza e le prestazioni dei sistemi ingegneristici.